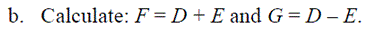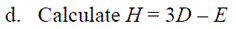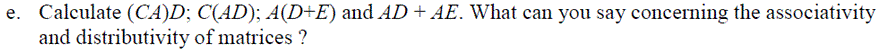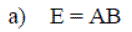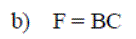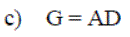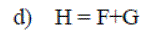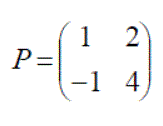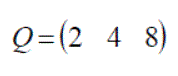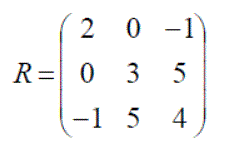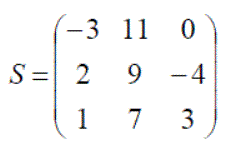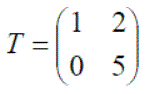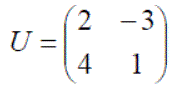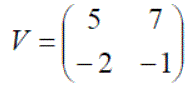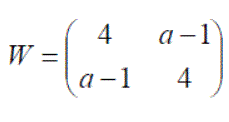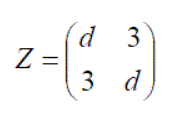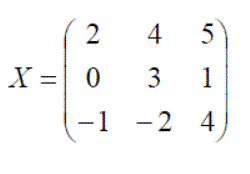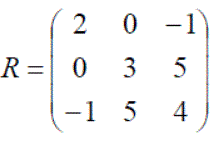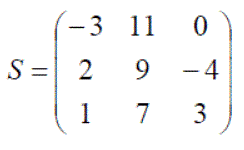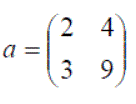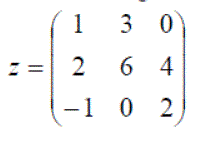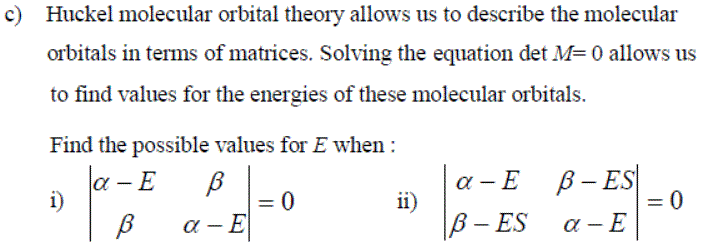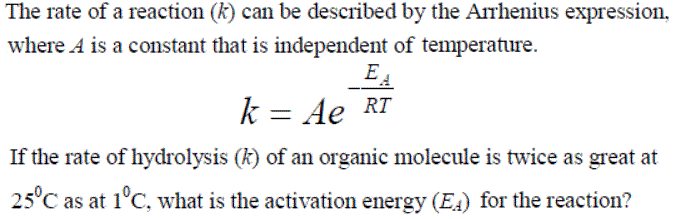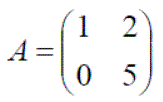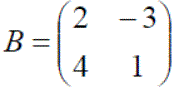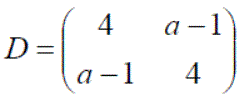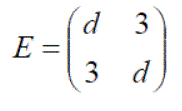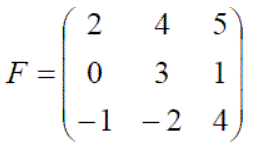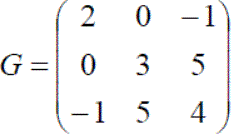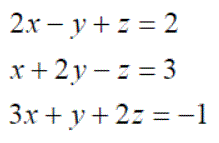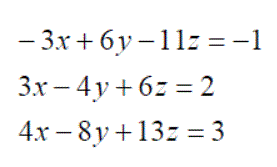Dimensions
A matrix is an array of elements comprising of n rows and m columns, where n and m are integers greater than or equal to 1. The matrix notation provides a way of collecting together sets of objects with a particular kind of inter-relationship. The advantage of a matrix formulation is that several mathematical tools can then be used to uncover further interesting properties and inter-relationships.
Matrices are referred to in terms of their number of rows and columns. For example a 3 by 2 matrix is one with 3 rows and 2 columns. This would usually be written as 3 x 2 matrix.
Matrices do not have to have the same number of rows and columns, but those that do are called square matrices.
Below are examples of different size matrices: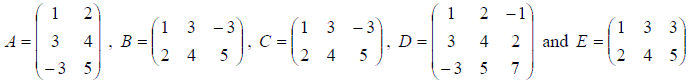
A is a 3 x 2 matrix, B a 2 x 3 matrix, C a 2 x 3 matrix, D a 3 x 3 matrix and E a 2 x 3 matrix.
In order to refer to certain element in a matrix the following notation is often used: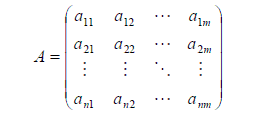
The first and the second subscript designate the row and the column in which the element is situated; i.e. element aij lies at the intersection of the ith row and jth column of the matrix.
Multiplication by a Constant, Addition & Subtraction
Two matrices X and Y are equal if they have the same dimensions and if xij = yij for all i, j.
Only matrices of same dimensions can be added or subtracted and the resulting matrix will have the same dimensions.
If Z = X ± Y then zij = xij ± yij for all i, j.
Example: For the five matrices given above only B, C and E have the save dimensions therefore only these can be added or subtracted, e.g.
A matrix can be multiplied by any ordinary number k according to the rule Z = kY with zij = k yij for all i, j. Example: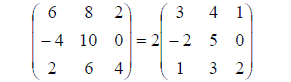
Properties of Matrix Addition and Scalar Multiplication:
Suppose A, B, and C are m × n matrices and c and k are scalars. Then
| A + B = B + A | (Commutativity) |
| A + (B + C) = (A + B) + C | (Associativity) |
| c(kA) = (ck)A | (Associativity) |
| A + 0 = A | (Zero Element) |
| c(A + B) = cA + cB | (Distributivity) |
| (c + k)A = cA + kA | (Distributivity) |
Multiplication of Matrices
An n x m matrix A and m x p matrix B can be multiplied together giving a n x p matrix C. It is important that the first matrix (A) has the same number of columns as the second (B) has rows.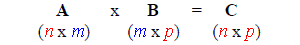
The elements in the matrix C are given by: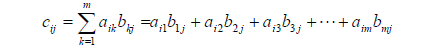
Example: A 3 x 2 matrix can be multiplied with a 2 x 3 matrix, giving either a 3 x 3 matrix or a 2 x 2 matrix (depending on the order of the multiplication):
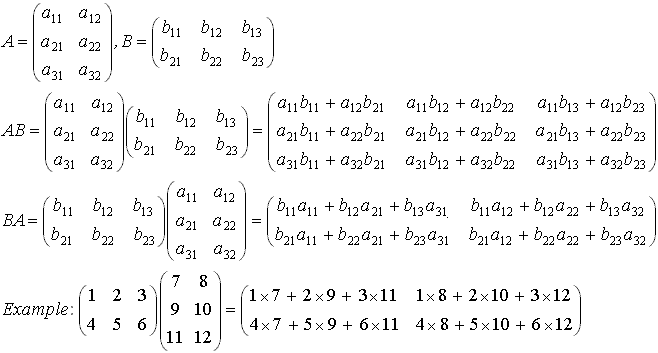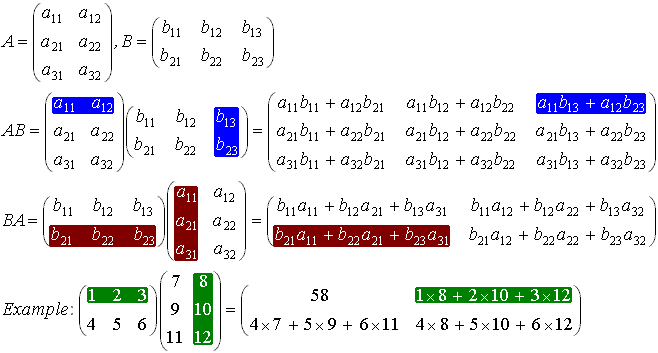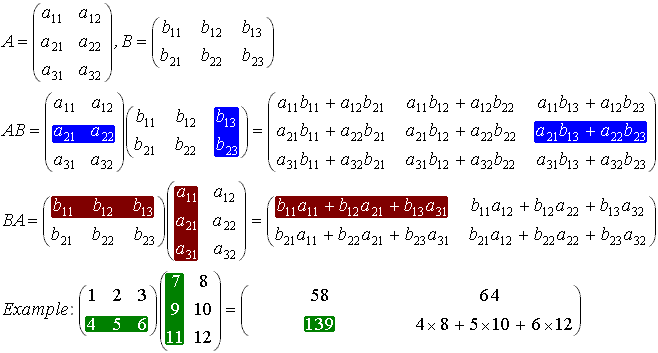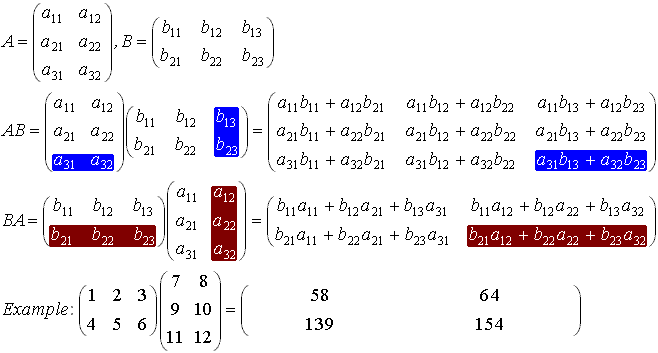
Transpose
The Transpose of a matrix A, AT, is obtained by interchanging the rows and columns of the matrix. The first Row of matrix A forms the first column of AT and so on, such that: (AT)ij = aji
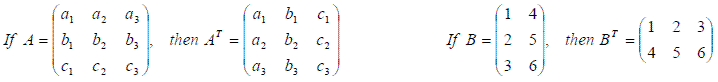
Determinant (detM or |M|)
The determinant is a value associated with a square matrix. It is generally computed from the entries of the matrix by a specific arithmetic expression.
The 2x2 Matrix: To find the determinant of a 2x2 matrix you must multiply the terms on the leading diagonal and
subtract the product of the terms on the other diagonal, i.e.:
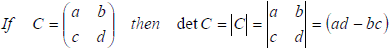
The 3x3 Matrix: To find the determinant of a 3x3 matrix we apply similar rules, first defining suitable 2x2 matrices and then finding the difference between the product of the two diagonals as above. The 2x2 matrices are chosen so that every column in the matrix is used in each term of the expression and the sign of the three terms alternates as you move across the columns in the table.
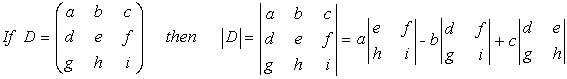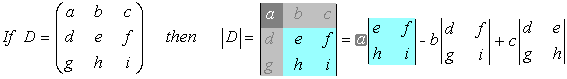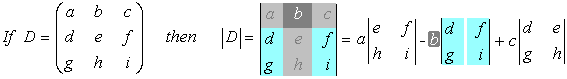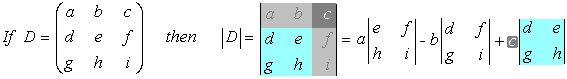
Note that you are unlikely to need to do calculations on any larger matrices, but the technique
follows the same trend for all sizes.
Cofactor (C)
The cofactors matrix is a matrix with the same dimensions as the original matrix (A). It is built following similar techniques as used to calculate the determinant.
The matrix of cofactors consists of elements called cofactors of determinants Cij. The cofactor Cij is obtained by deleting the ith row and jth column of the matrix A to form an (n-1)x(n-1) determinant, which is then multiplied by (-1)i+j
The 2x2 Matrix:
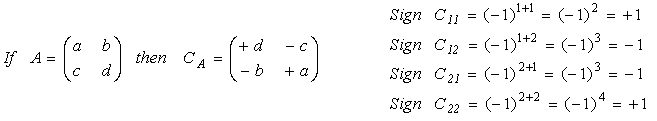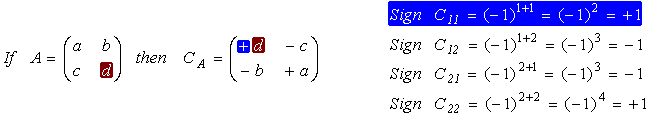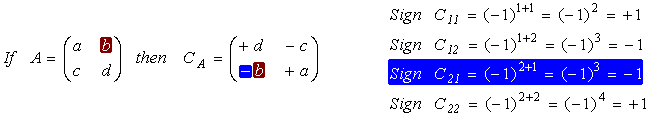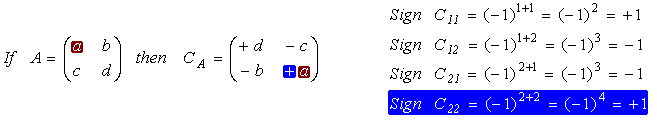
The 3x3 Matrix:
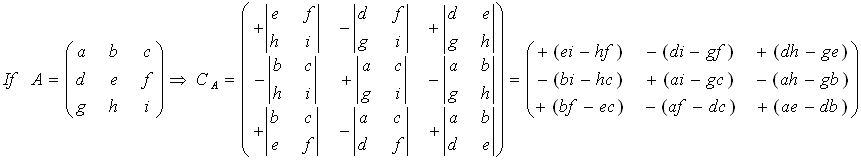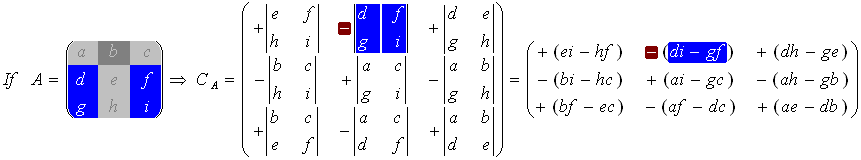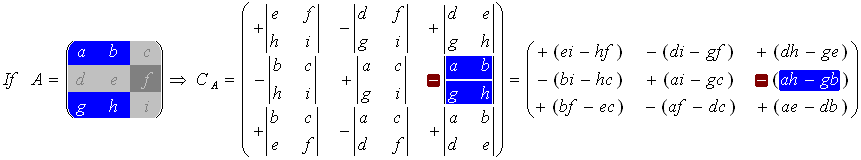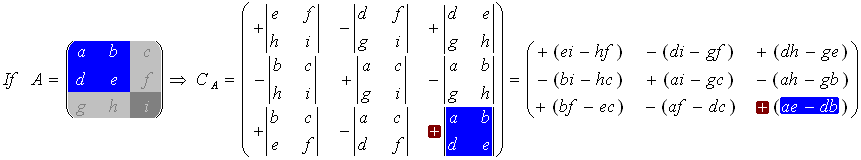
Inverse
Given a square matrix A we can define an inverse matrix A-1 which satisfies the equality AA-1=I, where I is the identity matrix.
| For example, if A is a 3x3 matrix, we have: | 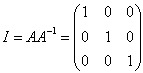 |
| We define the Inverse matrix A | 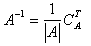 |
where |A| is the determinant of matrix A and CTA is the transpose of the cofactors matrix of A.
| Example: Determining A-1 for the matrix | 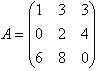 |
1. Find the determinant of A:
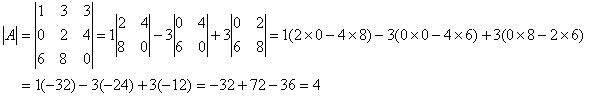
2. Determine the cofactors matrix of A:
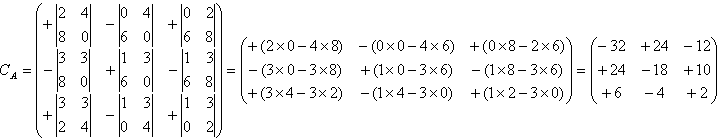
| 3. Write down the transpose of CA: | 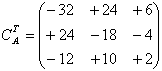 |
| 4. Put it all together: | 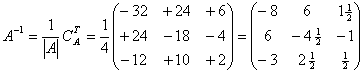 |
You can check that you have successfully determined the inverse matrix (A-1), by multiplying by the original matrix (A) and checking that this results in the Identity matrix (I), e.g.
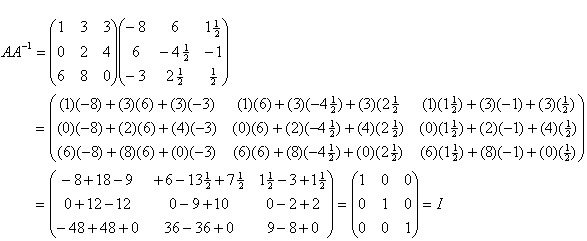
Important Note: the inverse of a matrix only exists for a square matrix and if |A| is not equal to zero.
Using Matrices to Solve Simultaneous Equations
Matrices can be used to solve simultaneous equations. All we need is to define a way to transpose a set of simultaneous equations into matrix form. Then we use the mathematical rules defined previously to find the solution of the simultaneous equations. In simultaneous equations we need as many equations as there are variables (i.e. for 1 variable (x) we need only one equation, for 2 variables (x and y) we need 2 equations, etc.).
In the case of 3 variables x, y and z we would have the following set of simultaneous equations:
ax + by + cz = d ex + fy + gz = h ix + jy + kz = l
| These can be written in matrix form as | 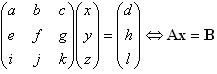 |
where A is the matric of coefficients, x is the matrix of variables and b is the column matrix of coefficients appearing on the right hand side of the set of equations.
If we now multiply both sides by A-1 we obtain A-1Ax = A-1b
Since the product A-1A gives the identity matrix (I) we can write x = A-1b, which provides the solution to the set of simultaneous equations.
Example: Given the following set of simultaneous equations:
x + 3y = 32 2x + 6y + 4z = 12 -x + 2z = 64
| We can write (in matrix form) | 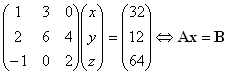 |
| The solution is given by | 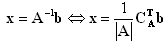 |
| And we can determine |A|=-12 and | 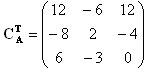 |
| So | 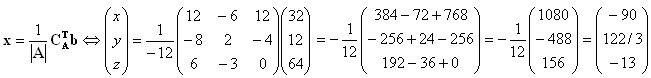 |
Therefore the values x=-90, y=122/3 and z=-13 satisfy the set of simultaneous equations.
Note on simultaneous equations: In a set of simultaneous equations if b is a matrix with only zeros then the set of simultaneous equations is referred to as homogeneous equations. If b is a matrix with values different that zeros then the set of equations is referred as inhomogeneous. Homogeneous equations play a central role in the modelling of the electronic structure of atoms and molecules and also in the related problem (for molecules) of determining the frequencies of the permitted nuclear motions.
Practice Exercises
Attempt each of the questions. Once you have an answer (or if you are having problems) - Click on the question to bring up the solution.
Exercise 1: Using the matices defined below, answer the following questions:
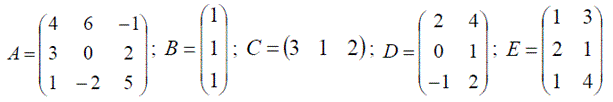
Exercise 2:
Exercise 3: HINT: There are 12 addition/subtraction combinations and 52 multiplication combinations:
Exercise 4: Using the following matrices, define E, F, G and H
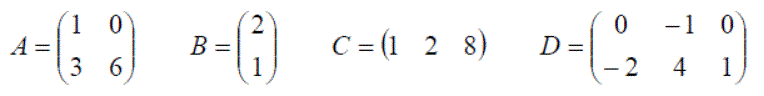
Exercise 5:
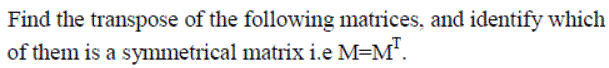
Exercise 6:
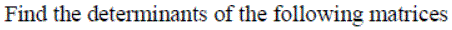
Exercise 7:
Exercise 8:
Exercise 9:
Exercise 10: Find the inverse of the following matrices, and verify for all matrices that M-1M = MM-1 = I
Exercise 11: For the following sets of simultaneous equations, write them in matrix format and find their solutions:
Exercise 12: