Introduction
A vector is a quantity which has both magnitude and direction, e.g. The effect a magnetic field has on a charged particle, diffusion of particles in solution, vibrational stretches in a diatomic molecule, etc.
Notation
A vector in 2 or 3 dimensional space can be represented by a directed line segment like those shown below:

- A vector will either be written in bold type (e.g. a), underlined (e.g. c) or with an arrow over the top (see diagram above).
- The arrow on the line indicates the direction of the vector.
- The length of the line represents the vectors magnitude.
- The magnitude of the vector (a) is it's modulus (|a|)
| Unit Vector: A unit vector is a vector of length 1 (unity), obtained by dividing the vector by it's modulus: |  |
Cartesian Components
Any vector in the x,y,z plane can be written in terms of these unit vectors and it's modulus found using Pythagorus' Theorem.
i represents a unit vector in the direction of the positive x axis. j represents a unit vector in the direction of the positive y axis. k represents a unit vector in the direction of the positive z axis.

Adding/Subtracting Vectors
The sum or difference between two vectors can be calculated by adding or subtracting their respective i,j,k values.
Subtraction of a vector is like addition of a vector in the opposite direction. Graphically this can be illustrated as shown below
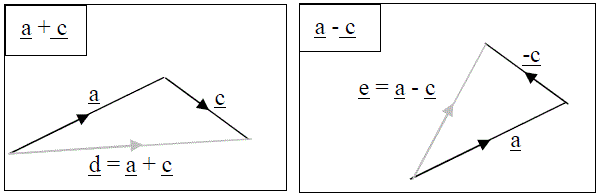
The Scalar Product / The Dot Product: Finding the angle between two vectors

The Vector Product / The Cross Product: Multiplying vectors yields a vector perpendicular to their plane

Practice Exercises
Attempt each of the questions. Once you have an answer (or if you are having problems) - Click on the question to bring up the solution.
The following defined vectors are used in Exercise 1, 2, and 3

Exercise 1: Addition and subtraction
Exercise 2: Unit vectors
Exercise 3: Scalar/Dot product
Exercise 4: Application














