THE PROBLEM

If you find that the version of Excel you are using does not have the Data Analysis Tools available:

FIRST check if this problem is down to the fact that the Analysis ToolPak has not been added - See the relevant instructions on the "Using Excel - Data Analysis" page for your version of Excel.

If the issue is NOT due to the Analysis ToolPak needing to be added - It is likely to be due to one of the following:

1. You are using Office Online, Excel 2013 for RT, Excel 2011 for Mac or Excel 2008 for Mac - These versions of Excel do not include/support the Analysis ToolPak.

2. You are using a version of Excel which does support the Analysis ToolPak; however this option was not selected during the original installation - This can be fixed by updating the installation, although this process often requires you to have the original Office installation disk.

Having a version/copy of Excel that is missing the Analysis ToolPak is potentially problematic in that it contains two Data Analysis Tools that will commonly be used for the analysis of data from practicals performed in the Level 4 Lab. These are:

• Descriptive Statistics - Used to determine the Mean and 95% Confidence Level for a set of readings.

• Regression - Used to determine the line of best fit (for a set of x and data), including evaluating the associated 95% Confidence Limits for the fitted parameters.

THE SOLUTION

A simplistic solution is to find a computer running a version of Excel that does have the Analysis ToolPak installed. However there is an alternative means of performing the core Descriptive Statistics and Regression Analyses (with associated error treatment) which can be performed on almost any version of Excel. Note: It has not yet been possible to test if this solution works for Office Online and versions of Excel prior to 2003.

DETERMINING THE MEAN WITH ITS ASSOCIATED 95% CONFIDENCE LEVEL

Note: Makes sure you hit [Enter] after inputting your formulas!

1. Enter your multiple readings in a column on your spreadsheet.

2. In the cell a couple below the last data value enter the formula   =AVERAGE(DataRange)   where DataRange is the cells containing the data.

   EXAMPLE: If the data was in Cells A2, A3, A4, A5 and A6 (as shown in the example image); then you would enter   =AVERAGE(A2:A6)   in Cell A8.

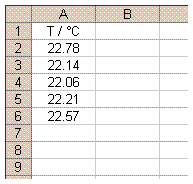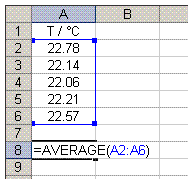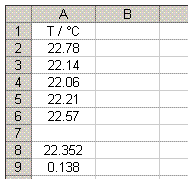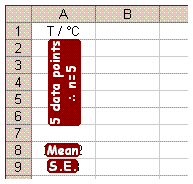
3. In the next cell below enter   =STDEV(DataRange)/SQRT(n)   where n is the number of data points.

   EXAMPLE: For the data shown you would enter   =STDEV(A2:A6)/SQRT(5)   in Cell A9.

   Note: In some versions of Excel the   STDEV   function has been replaced by the   STDEV.S   function, i.e. for the data shown you would need to enter   =STDEV.S(A2:A6)/SQRT(5)   in Cell A9.

4. The two functions you have used calculate the Mean and the Standard Error (SE) of the Mean. However, we want the 95% Confidence Level rather than the SE. The 95% Confidence Level is found by multiplying the SE by the appropriate t_95% value, which itself is found from a table of t-Values.

   EXAMPLE:
   
   The data shown has a Mean of 22.352 ^oC and an associated Standard Error of 0.138.
   
   Degrees of Freedom is defined as n-1; so since there are 5 data points (n) we have 4 Degrees of Freedom.
   
   From the t-value table, for 4 Degrees of Freedom, t_95% is 2.776.
   
   Therefore the 95% Confidence Level for the Mean of the data shown would be   = SE*t_95% = 0.138*2.776 = 0.383   and the final cited result would be   Average Temperature = 22.4 ± 0.4 ^oC.

LINEAR REGRESSION

Note: If all you need to obtain is the line of best fit, i.e. you do not need to determine the 95% Confidence Limits of the fitted parameters, this can be achieved by plotting the data and adding a linear equation - See the relevant instructions on the "Using Excel - Add a Trendline" page for your version of Excel.

1. Enter the x and y data into adjacent columns on your spreadsheet. In the example below Times (in minutes) are being used as the x values and Temperatures (in Kelvin) are being used as the y values.

2. In the cell a couple below the last value of the first column of data, enter the formula   =LINEST(DataRangeY,DataRangeX,,TRUE)   where DataRangeY is the cells containing the y values and DataRangeX is the cells containing the x values to be used in the Regression.

   EXAMPLE: If your y values were in Cells B2 to B8 and your x values in A2 to A8; then you should enter   =LINEST(B2:B8,A2:A8,,TRUE) in Cell A10.

3. Highlight a 2x2 block of cells, with the formula you have entered in the top left cell.

   EXAMPLE: For the sheet shown below, you would highlight the four cells A10 to B11.

4. There are different instructions for the next step, depending on whether you are using Windows or a Mac:
   

   USING WINDOWS	USING A MAC
   Press   F2	Press   control + U
   then press    Ctrl + Shift + Enter	then press     (command) + return

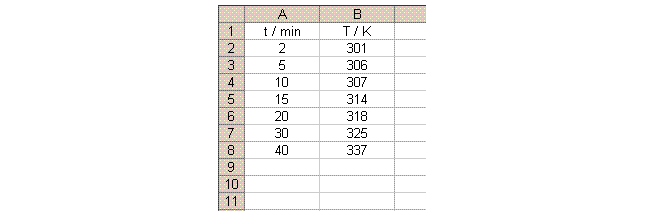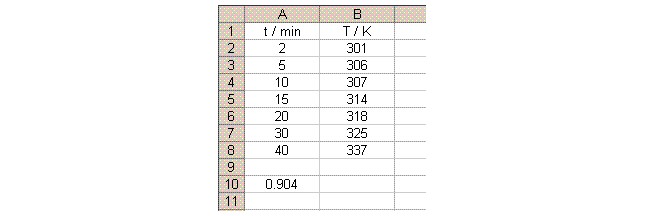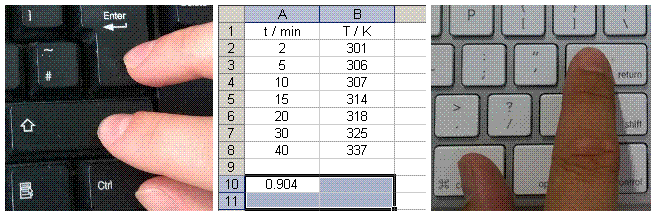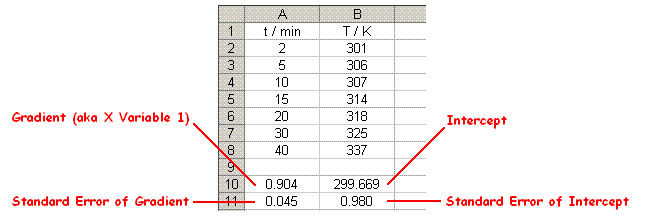
   ADDITIONAL NOTE FOR USERS OF OFFICE 2013 FOR RT: Surface RT's do not have an F2 button; in place of this step you should instead press    Fn +

5. The values that will appear in the four highlighted cells are:
   
   
   • Top Left = Gradient. (Appears in Coefficients column of X Variable 1 row when performing the Regression procedure using the Data Analysis Tool.)
     
     
   • Bottom Left = Standard Error of the Gradient. (Appears in Standard Error column of X Variable 1 row when performing the Regression procedure using the Data Analysis Tool.)
     
     
   • Top Right = Intercept. (Appears in Coefficients column of Intercept row when performing the Regression procedure using the Data Analysis Tool.)
     
     
   • Bottom Right = Standard Error of the Intercept. (Appears in Standard Error column of Intercept row when performing the Regression procedure using the Data Analysis Tool.)

   The 95% Confidence Levels for the Gradient and Intercept can then be found by multiplying their Standard Error by the appropriate t_95% value, which is found from a table of t-Values.

   EXAMPLE:
   
   For the data shown the Gradient has been determined as 0.904 Kmin^-1 with a Standard Error of 0.045; and the Intercept has been determined as 299.669 K with a Standard Error of 0.980.
   
   Since there are 7 data points (n), there are 6 Degrees of Freedom (n-1).
   
   From the t-value table, for 6 Degrees of Freedom, t_95% is 2.447.
   
   Therefore the 95% Confidence Level for the determined Gradient would be   = SE*t_95% = 0.045*2.447 = 0.110   and the final result could be cited as    Gradient = 0.9 ± 0.1 Kmin^-1.
   
   Similarly the 95% Confidence Level for the Intercept would be   = SE*t_95% = 0.980*2.447 = 2.398    with a final cited result of    Intercept = 299.7 ± 2.4 K.

Note: If you wish to perform a Regression where the constant is set to zero (i.e. y = mx) - In step 2 use the formula    =LINEST(DataRangeY,DataRangeX,FALSE,TRUE)