WEB TUTORIAL - Group Theory

The Reduction Forumla

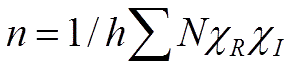
Each part is important and will have a value to input:

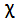• _R and 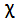_I are the characters of the reducible and irreducible representations.

  The reducible representations you work out yourself and are the 'number of unchanged bonds'.
  The irreducible representations are found in the Character Table.

• N is the coefficient in front of each of the symmetry elements on the top row of the Character Table.
• h is the order of the group and is the sum of the coefficients of the symmetry element symbols (i.e. h = ΣN). The summation of the Reduction Formula is carried out over each of the columns in the Character Table for the irreducible representation under consideration.
• n is the number of times that the row representation will appear in the IR or Raman spectra.

IMPORTANT NOTES:

The Reduction Formula ALWAYS gives either 0 or a positive integer value. If this is not the case when you perform the calulation you have gone wrong somewhere. Often it is an arithmetic slip up, or commonly an incorrectly worked out _R value.

An Example of the Reduction Formula in action: For the C_2v character table row A₁

C2v	E	C2 (z)	v(xz)	v(yz)	Linear functions, rotations	Quadratic functions	Cubic functions
A1	+1	+1	+1	+1	z	x2, y2, z2	z3, x2z, y2z
A2	+1	+1	-1	-1	Rz	xy	xyz
B1	+1	-1	+1	-1	x, Ry	xz	xz2, x3, xy2
B2	+1	-1	-1	+1	y, Rx	yz	yz2, y3, x2y

Number of symmetry elements, h = 4

Where h = 4 and _R values (for the number of unchanged bonds when a symmetry element is performed) are 2, 0, 2, 0.

Apply to row A₁:
Numbers in the round brackets indicate (N x _R x _I)
1/4[ (1 x 2 x 1) + (1 x 0 x 1) + (1 x 2 x 1) + (1 x 0 x 1) ] = 1/4 x (4) = 1