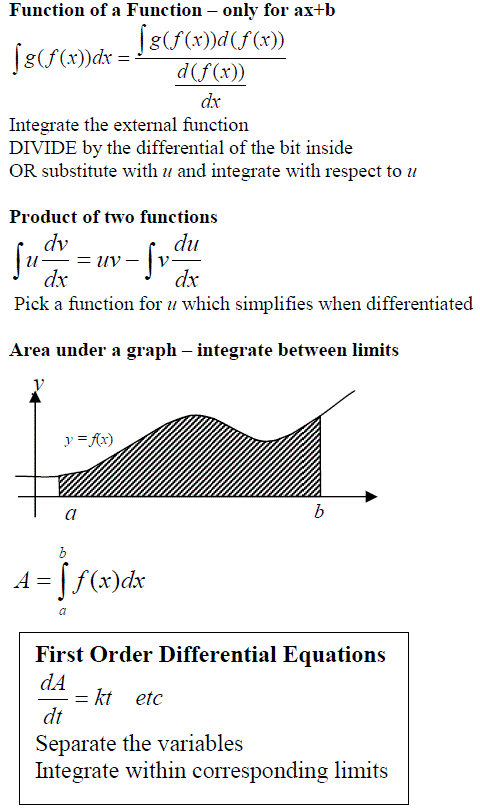Background
In physical chemistry we try to represent measured quantities of some variable (say, temperature or pressure) by a function. This allows us to interpolate between the measured points to find a value for a point not measured, and extrapolate to find a value for a point outside the range.
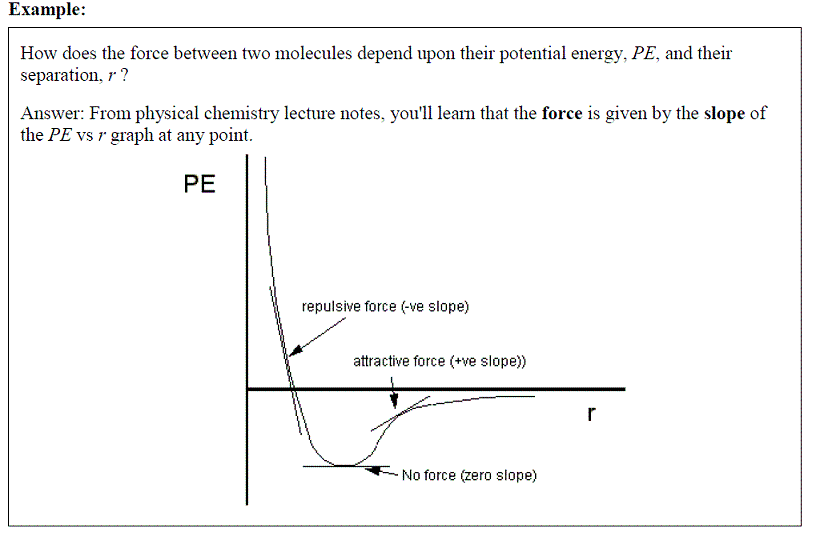
EXAMPLE: How is the pressure of a gas related to other measurable properties, such as volume and
temperature?
ANSWER: The Ideal Gas Equation, P = nRT / V where the pressure, p, is defined as a function of 3 variables: the number of moles of gas (n), the temperature of the gas (T) and the volume of the gas (V). Note: R is a constant ( = 8.314 J K-1 mol-1)
Rates of Change
Things in Chemistry rarely stay stationary so normally we are interested in looking at how properties change with respect to each other.
| Definition: Calculus is the study of the rate of change of one quantity with another |
pressure wrt temperature dp/dT pressure wrt volume dp/dV
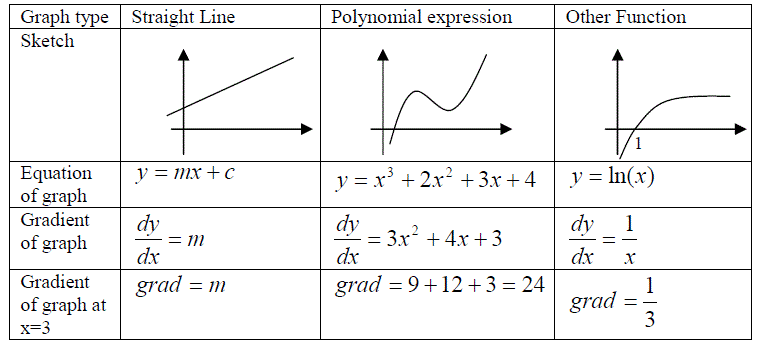
Changes are often observed as gradients of graphs,
i.e. gradient = (y2 - y1) / (x2 - x1) = (change in y) / (change in x) = dy/dx
The gradient can be determined either by measurement, i.e. by plotting the graph and drawing a tangent to an appropriate point, or by using a mathematical formulae to define the gradient at a given value of x and y.
Formal Derviation of the Magic Formula
| Consider a graph - this represents the relationship between two quantities with respect to one another. The rate of change of the two quantities with respect to each other at any value of a quantity is represented by the gradient of the graph linking the two quantities at this value, i.e. Dy/Dx = gradient Consider two points on the graph one a short distance from the other | 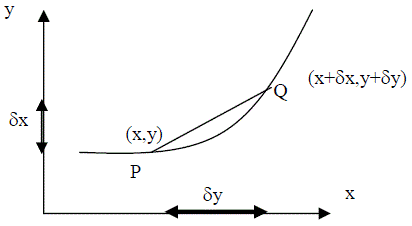 |
| Thus we have points (x, y) and (x+dx, y+dy) and the gradient of the chord P,Q is given by: | 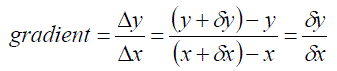 |
As P gets closer to Q, the gradient of the chord becomes closer to the gradient of the tangent at that point on the graph.
Let us now consider if y = f(x) P = (x, f(x)) Q = (x+dx, f(x+dx))
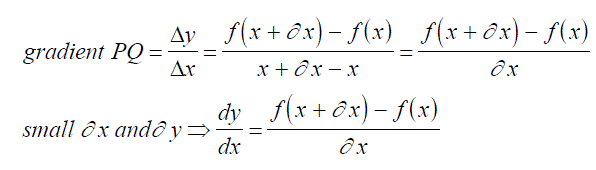
We can then calculate an expression for the gradient at any part of the graph, for example x3
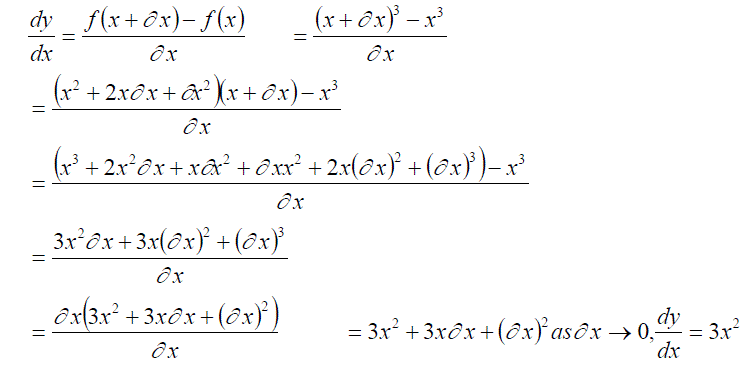
More simply we would normally follow the given formula (used for all but a few complex examples):
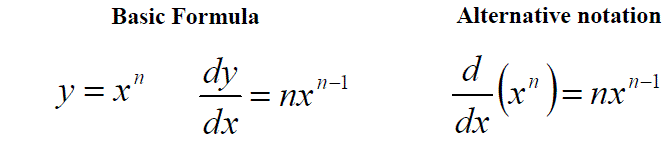
Stationary Points
Differentiation of a function yields a general expression for the gradient of that graph at any point.
| A stationary point on a graph is a point where the gradient of the graph is zero. Points fall into three categories: Minimum, Maximum, Point of inflexion. | 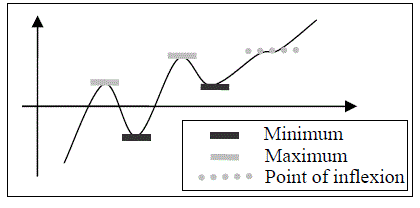 |
1. Differentiate the function to give you the general expression for the gradient.
2. Solve the equation for when the expression = zero, i.e. dy/dx = 0
How to Identify a Stationary Point
1. Differentiate the expression a second time (to give you d2y/dx2)
2. The stationary point is a minimum if d2y/dx2 > 0
3. The stationary point is a maximum if d2y/dx2 < 0
4. The stationary point is a point of inflexion if d2y/dx2 = 0
| EXAMPLE: | y = x3 + 4x2 + 5x + 2 | dy/dx = 3x2 + 8x + 5 |
| Stationary point: dy/dx = 0 | 0 = 3x2 + 8x + 5 = (3x + 5)(x + 1) | Therefore x = -1, -5/3 |
| Second derivative: | d2y/dx2 = 6x + 8 | |
| For x = -1 | d2y/dx2 = 2 | Therefore a Minimum |
| For x = -5/3 | d2y/dx2 = -2 | Therefore a Maximum |
Function of a Function, Products & Quotients

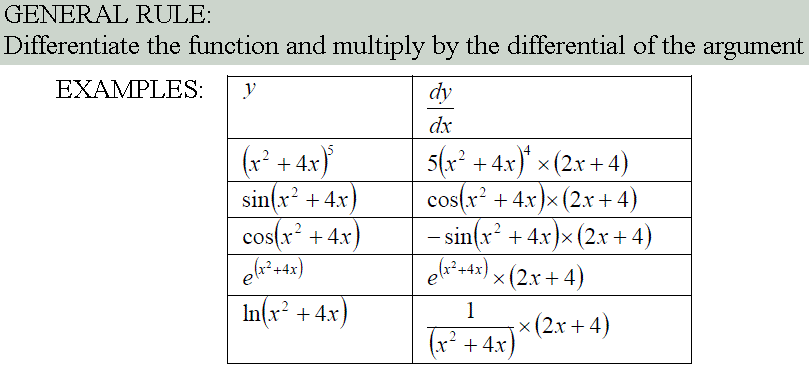

Non-Polynomial Functions
As has been show previously, the general formula for the differentiation of a polynomial expression, f(x) = axn, can be written as: df(x)/dx = anxn-1
However not all functions are polynomial expressions. The most common non-polynomial functions are: exp(x), ln(x), sin(x), cos(x) and tan(x). These functions also have a formula for differentiating them.


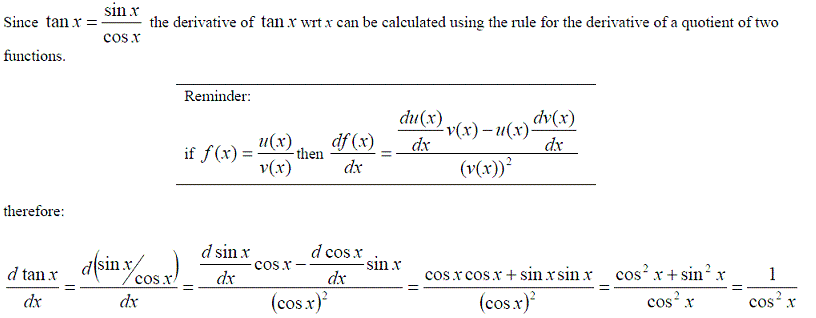

Example 1: The derivative of f(x) = 3e4x, is df/dx = 3 x 4 x ex = 12ex
Example 2: The derivative of f(x) = 3e4x+5
is 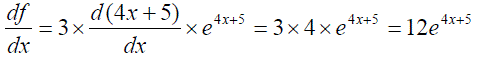
Example 3: The derivative of f(x) = 2ln(3x2+5x),
is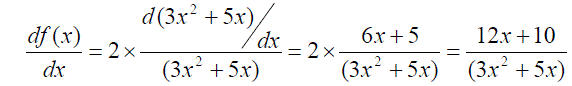
Example 4: The derivative of f(x) = 3sin(2x2+3),
is 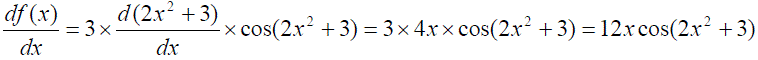
Differential Equations– Rates of Reactions
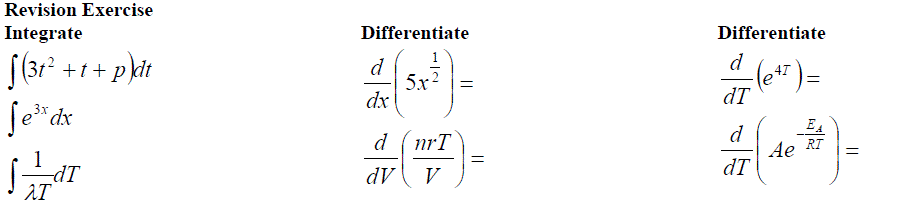
Solving First Order Differential Equations
We have met previously the inverse relationship between integrating and differentiating functions.
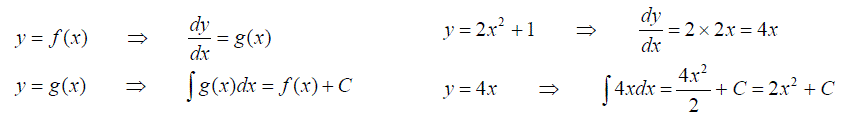
And can recognise that if we are told that

Then it follows that
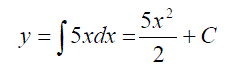
Equation (a) is a “ First order Differential Equation”, a relationship involving x, y and the derivate of y with respect to x.
Chemical equations will often appear in this form, containing the derivatives themselves, if we are monitoring the change in a reaction etc
For simple relationships, such as the one presented in equation (a) you can recognise that if you integrate this expression you should return a value for y, however a more general method by which we can reach this solution, is available, which is applicable to a whole range of functions.

Expressions including the other variable
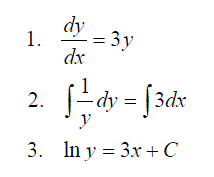
Expressions with Both Variables
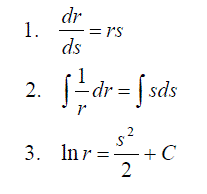
Applications to Rates of Reactions
Often in chemistry we are concerned with the rate at which a reaction proceeds. This quantity can be calculated by observing the rate of change of the concentration of the reagents throughout the experiment – titrations at different time slots, level of fluorescence from an optically active compound.
Commonly the rate of the reaction will be related to the concentrations of the reagents in one of the formats illustrated below.
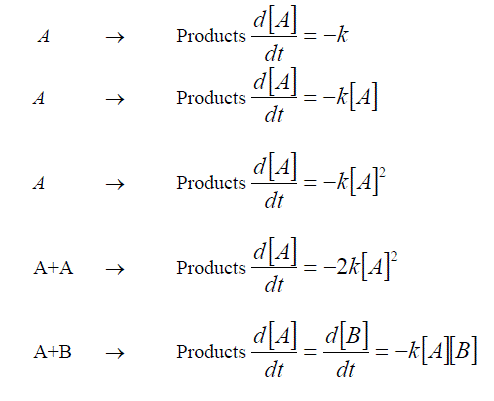
Enzyme reactions under some conditions
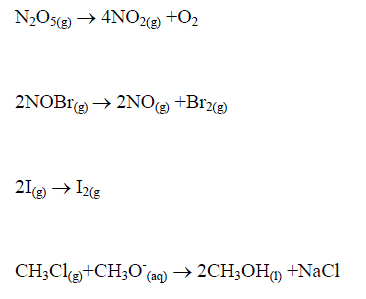
These equations are all first order differential equations and can all be solved according to the method of “Separating the variables”
Example 1:
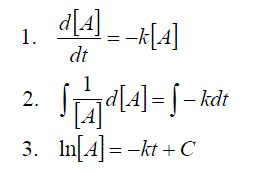
If we monitor the change in concentration of species A from [A]0 to [A]t over an experiment from time t0 to time t, then the evaluation becomes.
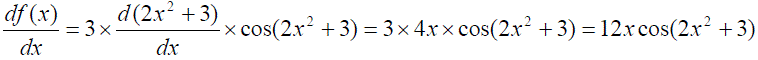
SUMMARY (WS13)
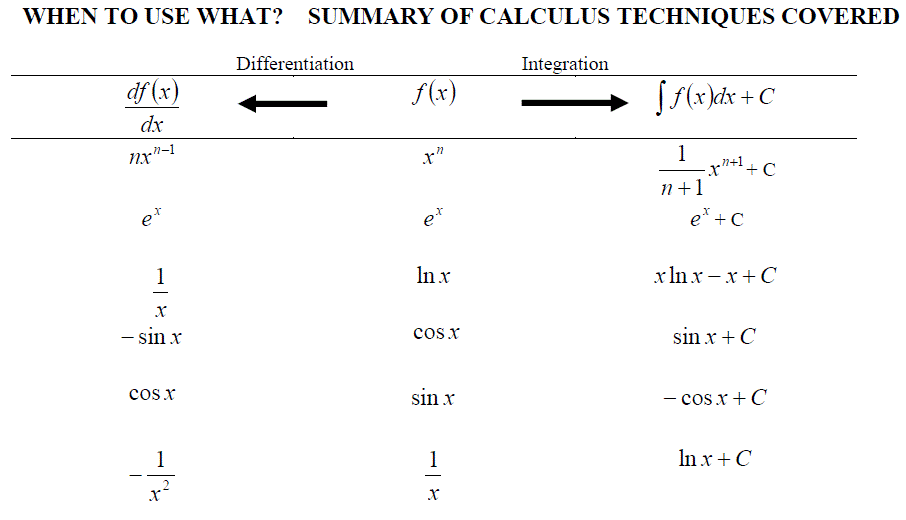

INTEGRATION