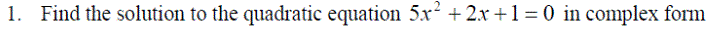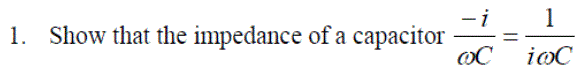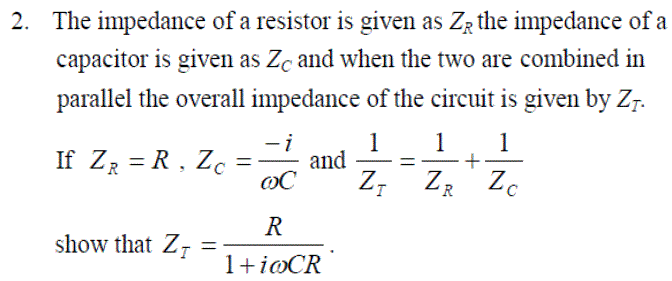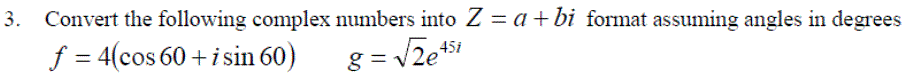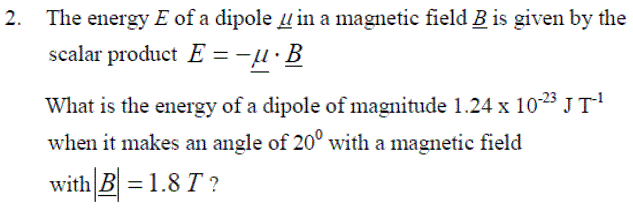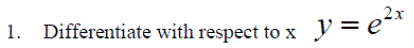Imaginary Numbers
It is impossible to determine the square root of a negative number ... if you try to find this on your calculator you will get an error message. However it becomes useful to construct a way in which we can write down square roots of negative numbers, which are known as imaginary numbers.
Definition of Imaginary numbers:
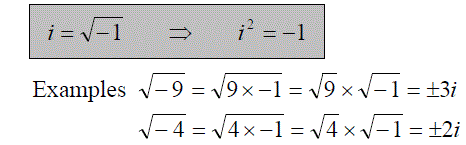
Complex Numbers
A complex number is made up of two parts, a real part (a) and an imaginary part (b), and is often denoted by the letter z: z = a + bi
| Examples: | General | 3 + 4i |
| Impedance of a capacitor and resistor in series | Z = R + 1/(iwC) | |
| Intensity of light from an AC modulating wave on a DC signal | I = IDC + IACeiwt |
Examples are also often encountered as the roots of quadratic equations,
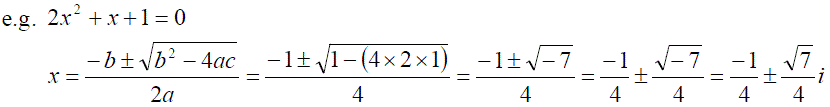
Addition/Subtraction of Complex Numbers
| Simply add or subtract the real and imaginary parts separately: | 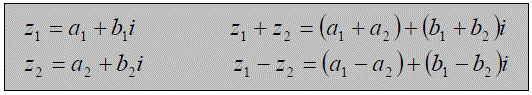 |
Example: If z1 = 2 + 3i and z2 = 5 + i then z1 + z2 = 7 + 4i and z1 - z2 = -3 + 2i
Multiplication of Complex Numbers
To multiply complex numbers, expand the brackets, remembering that i2 = -1.
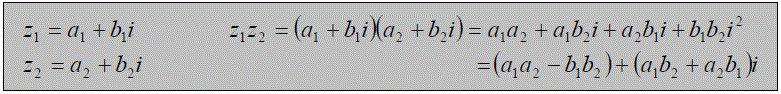
Example: If z1 = 2 + 3i and z2 = 5 + i
then z1z2 = (2 + 3i)(5 + i) = 10 + 2i + 15i + 3i2 = 10 + 17i - 3 = 7 + 17i
Complex Conjugates
| The product of a complex number and its complex conjugate returns a real number.
To find the complex conjugate (denoted with *) of a complex number, replace i with -i. |  |
Example: If z1 = 2 + 3i then z1* = 2 - 3i
and z1z1* = (2 + 3i)(2 - 3i) = 4 + 6i - 6i - 9i2 = 4 + 9 = 13
Division of Complex Numbers (using Complex Conjugates)
To divide one complex number by another we must multiply both top and bottom of the expression by the complex conjugate in order to maintain a real number on the base of the expression.

The Argand Diagram
| Complex numbers can be pictorially represented on an Argand diagram. The graph has two axis: The Real axis (Horizontal) and the Imaginary axis (Vertical). The complex number z = a + bi can then be plotted as a point with coordinates (a,b). |  |
| Example: The complex numbers 2 + 3i , -3 + 2i , -3 - 2i , 2 - 5i , 6 and i are shown plotted on the Argand diagram opposite. | 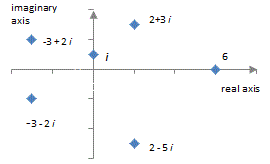 |
Polar Representation of Complex Numbers
Alternatively a complex number can be represented by a line joining (a, b) to the origin.

The complex number is defined by two parameters:
- The modulus of the complex number, which is the length of the line connecting (a, b) to the origin.

- The argument of the complex number, which is the angle of the line connecting (a, b) to the origin and real axis.

| And hence by trigonometric rules, the complex number can be written as | 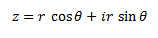 |
The Exponential Form of a Complex Number
| Eulers relations state that | 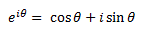 |
| Hence the polar form of a complex number | 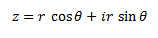 |
| can be written in exponential format as | 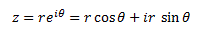 |
This format is often used to describe the ac component of an electromagnetic wave, e.g. in illumination the intensity of a fluctuating light beam is given as I = I0eiwt.
Converting between different forms of Complex Numbers
Example: Express z = 3 + 4i in polar and exponential format, using degrees and radians

Practice Exercises
Attempt each of the questions. Once you have an answer (or if you are having problems) - Click on the question to bring up the solution.
Exercise 1:Basic Calculations
Exercise 2:Applications
Exercise 3:Conversion of complex numbers
Exercise 4:Revision of other topics
Exercise 5:Application of polar complex numbers