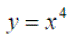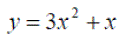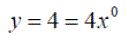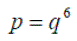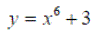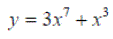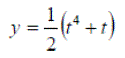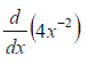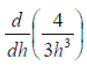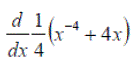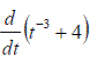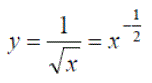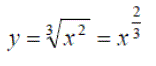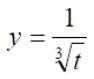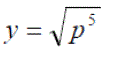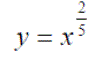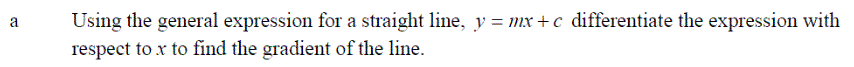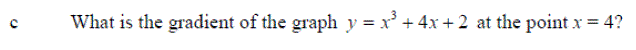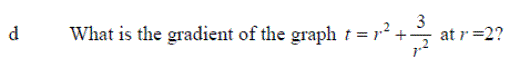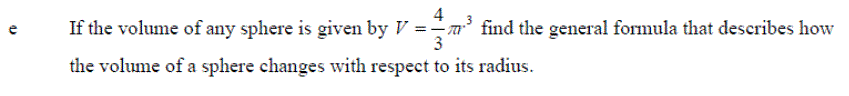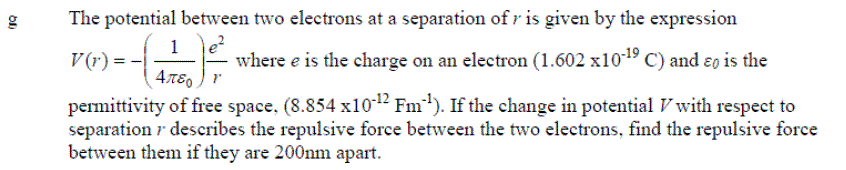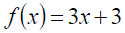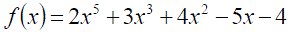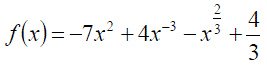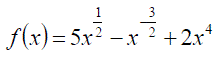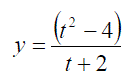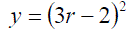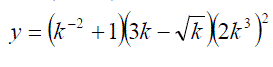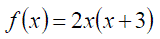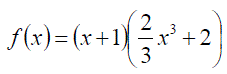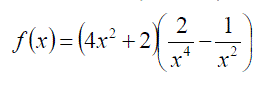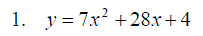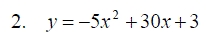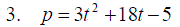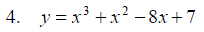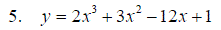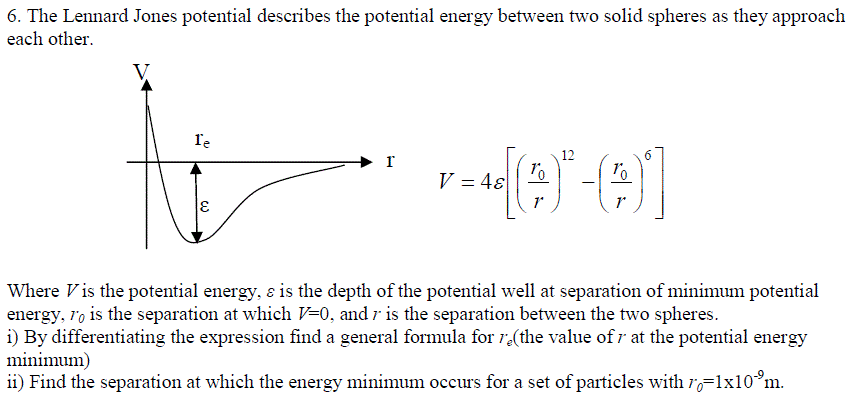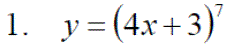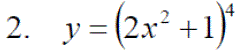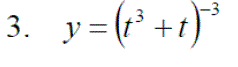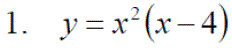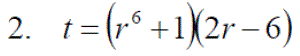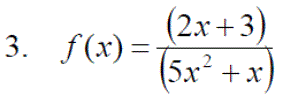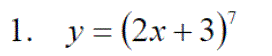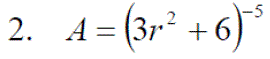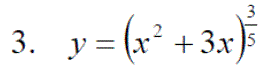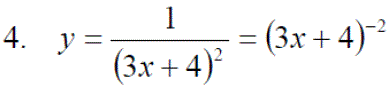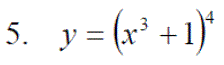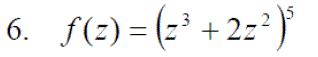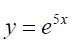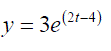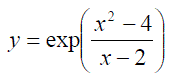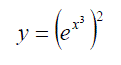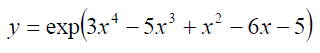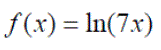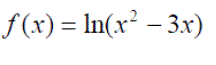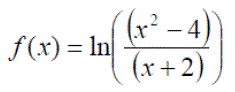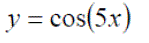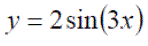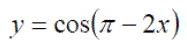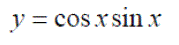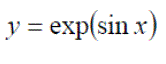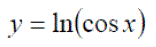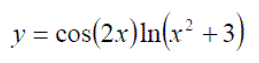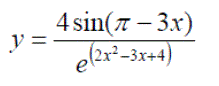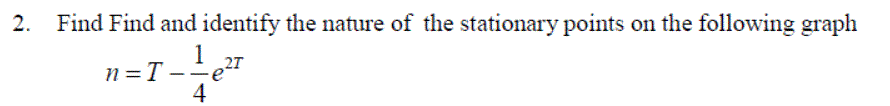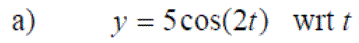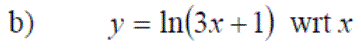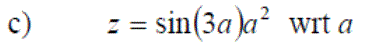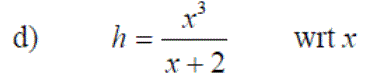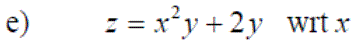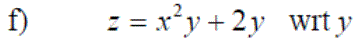Background
In physical chemistry we try to represent measured quantities of some variable (say, temperature or pressure) by a function. This allows us to interpolate between the measured points to find a value for a point not measured, and extrapolate to find a value for a point outside the range.
EXAMPLE: How is the pressure of a gas related to other measurable properties, such as volume and
temperature?
ANSWER: The Ideal Gas Equation, P = nRT / V where the pressure, p, is defined as a function of 3 variables: the number of moles of gas (n), the temperature of the gas (T) and the volume of the gas (V). Note: R is a constant ( = 8.314 J K-1 mol-1)
Rates of Change
Things in Chemistry rarely stay stationary so normally we are interested in looking at how properties change with respect to each other.
| Definition: Calculus is the study of the rate of change of one quantity with another |
pressure wrt temperature dp/dT pressure wrt volume dp/dV
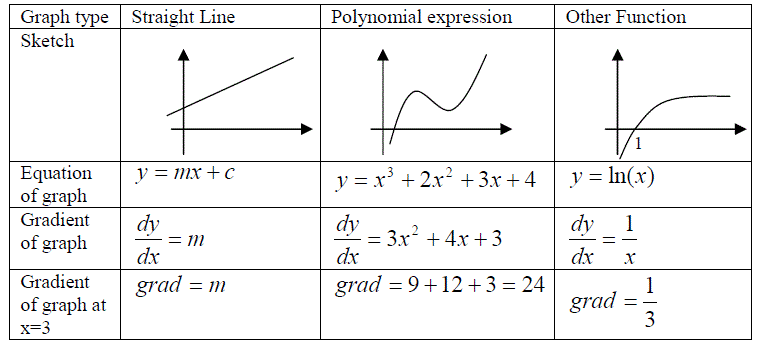
Changes are often observed as gradients of graphs,
i.e. gradient = (y2 - y1) / (x2 - x1) = (change in y) / (change in x) = dy/dx
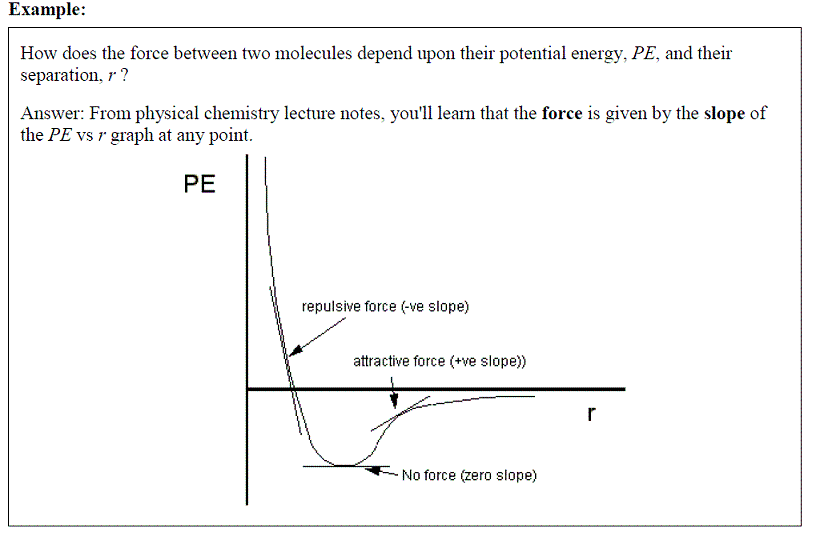
The gradient can be determined either by measurement, i.e. by plotting the graph and drawing a tangent to an appropriate point, or by using a mathematical formulae to define the gradient at a given value of x and y.
Formal Derviation of the Magic Formula
| Consider a graph - this represents the relationship between two quantities with respect to one another. The rate of change of the two quantities with respect to each other at any value of a quantity is represented by the gradient of the graph linking the two quantities at this value, i.e. Dy/Dx = gradient Consider two points on the graph one a short distance from the other | 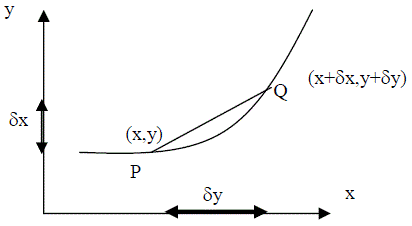 |
| Thus we have points (x, y) and (x+dx, y+dy) and the gradient of the chord P,Q is given by: | 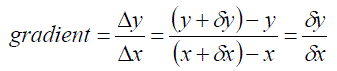 |
As P gets closer to Q, the gradient of the chord becomes closer to the gradient of the tangent at that point on the graph.
Let us now consider if y = f(x) P = (x, f(x)) Q = (x+dx, f(x+dx))
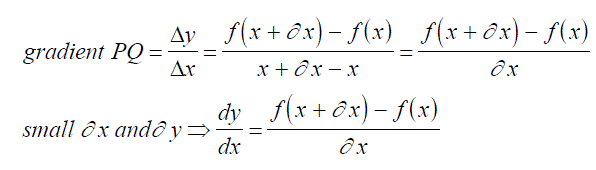
We can then calculate an expression for the gradient at any part of the graph, for example x3
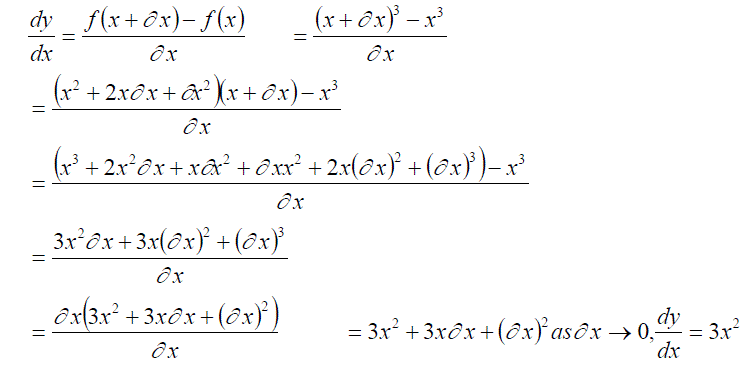
More simply we would normally follow the given formula (used for all but a few complex examples):
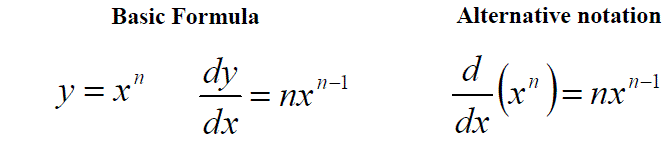
Stationary Points
Differentiation of a function yields a general expression for the gradient of that graph at any point.
| A stationary point on a graph is a point where the gradient of the graph is zero. Points fall into three categories: Minimum, Maximum, Point of inflexion. | 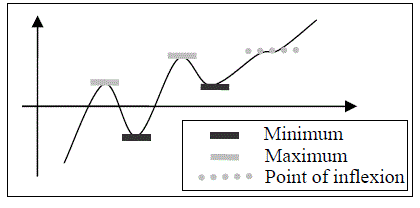 |
1. Differentiate the function to give you the general expression for the gradient.
2. Solve the equation for when the expression = zero, i.e. dy/dx = 0
How to Identify a Stationary Point
1. Differentiate the expression a second time (to give you d2y/dx2)
2. The stationary point is a minimum if d2y/dx2 > 0
3. The stationary point is a maximum if d2y/dx2 < 0
4. The stationary point is a point of inflexion if d2y/dx2 = 0
| EXAMPLE: | y = x3 + 4x2 + 5x + 2 | dy/dx = 3x2 + 8x + 5 |
| Stationary point: dy/dx = 0 | 0 = 3x2 + 8x + 5 = (3x + 5)(x + 1) | Therefore x = -1, -5/3 |
| Second derivative: | d2y/dx2 = 6x + 8 | |
| For x = -1 | d2y/dx2 = 2 | Therefore a Minimum |
| For x = -5/3 | d2y/dx2 = -2 | Therefore a Maximum |
Function of a Function, Products & Quotients

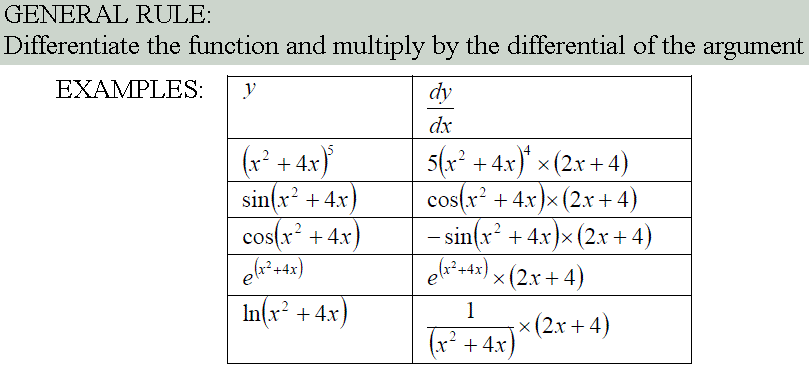

Non-Polynomial Functions
As has been show previously, the general formula for the differentiation of a polynomial expression, f(x) = axn, can be written as: df(x)/dx = anxn-1
However not all functions are polynomial expressions. The most common non-polynomial functions are: exp(x), ln(x), sin(x), cos(x) and tan(x). These functions also have a formula for differentiating them.

TANGENT:
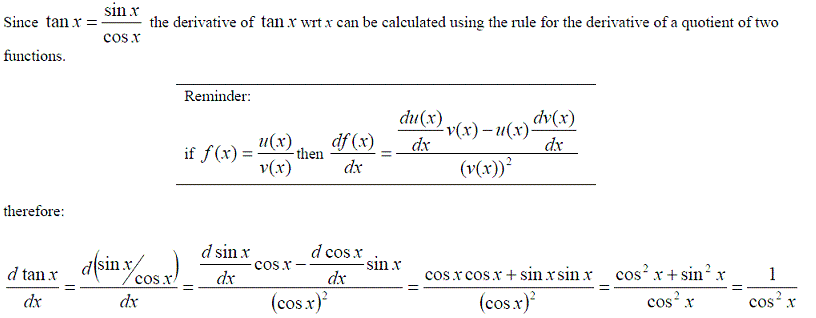

Example 1: The derivative of f(x) = 3e4x, is df/dx = 3 x 4 x ex = 12ex
Example 2: The derivative of f(x) = 3e4x+5
is 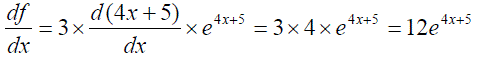
Example 3: The derivative of f(x) = 2ln(3x2+5x),
is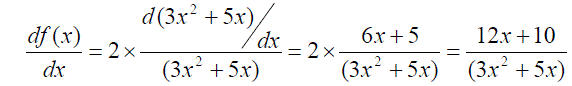
Example 4: The derivative of f(x) = 3sin(2x2+3),
is 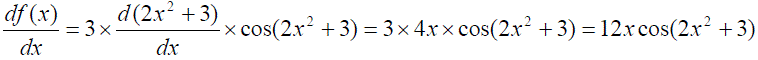
Summary

Practice Exercises
Attempt each of the questions. Once you have an answer (or if you are having problems) - Click on the question to bring up the solution.
Exercise 1:Differentiate the following expressions:
Exercise 2: Evaluate the following:
Exercise 3: Differentiate the following expressions:
Exercise 4:
Exercise 5: Differentiate the following:
Exercise 6: Find and identify the stationary pionts on the following graphs:
Exercise 7:
Exercise 8:
Exercise 9: Differentiate the following with expanding the brackets:
Exercise 10: Differentiate the following with expanding the brackets:
Exercise 11: Differentiate the following with expanding the brackets:
Exercise 12: Calculate the derivative of the following:
Exercise 13: Calculate the derivative of the following:
Exercise 14: Calculate the derivative of the following:
Exercise 15: Calculate the derivative of the following:
Exercise 16:
Exercise 17:
Exercise 18: Differentiate the following: