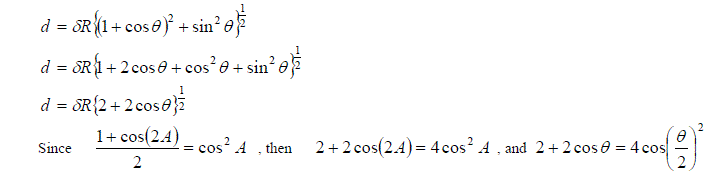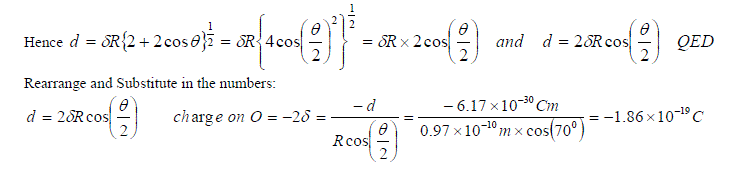Definition • Powers, Exponentials & Logarithms • Manipulation of Powers • Relationship between Logarithms and Exponentials • Manipulation of Logarithms • Trigonometric Functions • Trigonometric Identities • Use of Trigonometric Identities in Calculations

Definition of a Function

When we see f(x) it means a function of x. x is the variable and f is a quantity dependant on x.

For example:

1. The speed of a car is a function of how far the accelerator pedal is depressed.
2. The area of a circle is a function of its radius, A(r) = pr²
3. In the expression  2y = x, y is a function of x.
4. pH is a function of concentration, pH = -log₁₀[C]

Powers, Exponentials & Logarithms

Manipulation of Powers

GENERAL RULE: Apply to combination of exponential or power terms with the same base number in an expression

  xⁿx^m = x^n+m      (xⁿ)^m = x^nm      xⁿ / x^m = x^n-m

Note also that:  1 / x = x^-1      (xy)ⁿ = xⁿyⁿ      e^x / e^2x = e^(x-2x) = e^-x

  but that  (x+y)ⁿ  is not equivalent to  xⁿ+yⁿ  and there is no simplification for  xⁿyⁿ

Relationship between Logarithms and Exponentials

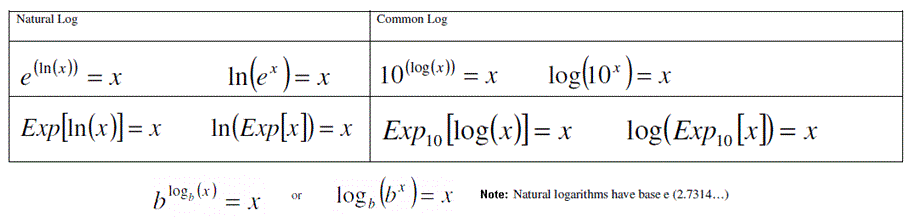
Manipulation of Logarithms

When applying logarithms to equations remember, as with any equation, you can do anything to one side of the equation as long as you perform the same function to the other side:

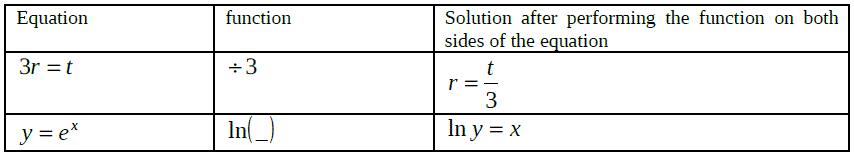
Example: Rates of reactions - The Arrhenius equation:

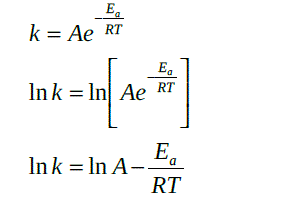A small rearrangement of the final answer enables us to recognise a straight line which we can plot from our data in order to find the activation energy and the Arrhenius constant.        i.e. a plot of  ln k  (y-axis) versus  1/T  (x-axis) will yield a straight line with  Gradient = -Ea/R  and  Intercept = ln c

Trigonometric Functions

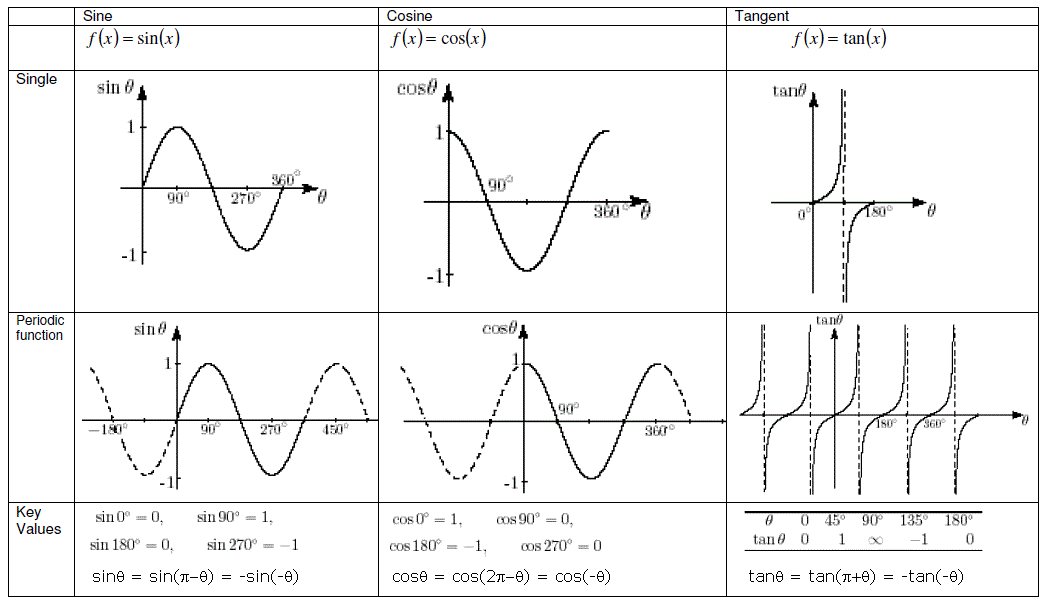
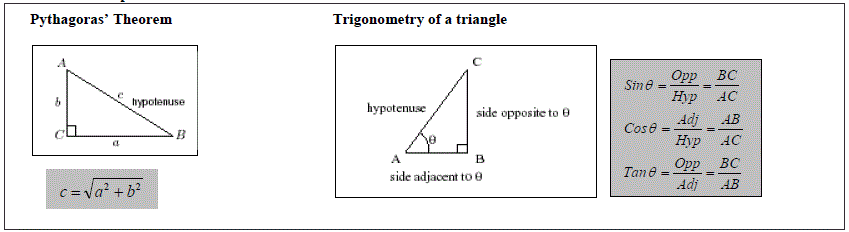
Trigonometric Identities

Special relationships exist between these functions, some of the most common are listed in the table below.

An extra rule - The Cosine Rule: For any triangle with three sides a, b, and c, and angles A (opposite side a), B (opposite side b) and C (opposite side c) the following applies:  a² = b² + c² - 2bccos(A)

The  sin²A + cos²A = 1  relationship can be easily visualised if we draw a circle

Use of Trigonometric Identities in Calculations

EXAMPLE: A molecule of water may be represented roughly as a triangle with charges {d, -2d, d}at the vertices. If the OH bond lengths are both equal to R, and the HOH bond angle is q, then the dipole moment in a water molecule can be described as follows:  d = dR{(1 + cosq)² + sin²q}^1/2
Show that the dipole moment is given by  d = 2dRcos(q/2)  and hence using the bond angle for water, the bond length and the value for the dipole moment given calculate the charge on the O atom.

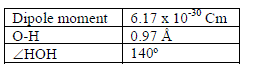
SOLUTION:

Mathematical Concepts - Contents